In this post, we solve Algebraic Equations by Iterative Method, which is also famously known as Successive Approximation Technique.
What is an Iterative Method?
Iterative Method:
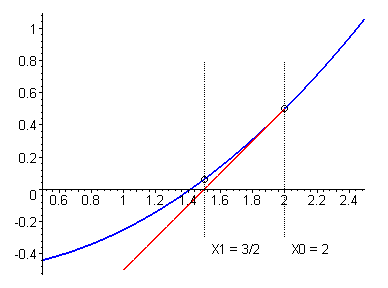
Consider the equation f(x)=0. We need to find the roots (approximate) of the equation.
Let x=g(x)-------------------------(1)
Firstly, assume an approximate root x0. The more accurate x0 is, the less the number of iterations for finding the exact root. We substitute x0 in (1) and get a new root x1. This process goes on and on, until we get a solution that matches the expected accuracy. We get a sequence of approximate roots. The convergence of the sequence depends on the value of x0 chosen initially. There are some conditions for the convergence of the method, which are not discussed here.
Where do we get the Source Code?
Right here!!!!!!!!!!!!!!
Source Code:
function iterateFunc(co,prev)
%Now 'co' is the vector under scrutiny
%'co' represents the coefficient vector
[a,b]=size(co);
% 'b' gives us the exact size of vector
% we iterate backward here
for i=b-1:-1:1
%we find the position corresponding to minimum degree
if co(i)~=0
min=i;
break;
end
end
% Beginning of truncation
% We truncate the constant and the terms with zero coeff:/
% near the constant
tco=co(1:min);
% Minimum degree to be taken as common is given by '(b-min)'
% b1 gives the size of truncated vector 'tco'
[a1,b1]=size(tco);
% infinite while loop
while 1
% Function return the value of polynomial after sub. of an user defined constant 'prev'
ans1=SubFunc(b1-1,tco,prev);
% Here find the entire right hand side
% and rise it to the power (reciprocal of min degree)
curr=((-co(b))/ans1)^(1/(b-min));
% when required accuracy of solution is met
% loop breaks
if abs(abs(prev)-abs(curr)) < 0.0000001
break;
end
% transfer from current to prev
prev=curr;
end
disp(curr);
end






4.JPG)






0 comments:
Post a Comment
தங்களது கருத்துக்களை இங்கே வெளியிடவும்...